NOTES

Here covering topics are: 1. Straight line equation, 2. DDA, 3. Bresenham line 

 

 

 Equation of a straight line -

m= (y2 - y1) / (x2-x1) = ∆y/∆x

∆y = m.∆x

∆x=∆y / m

m = slope

x,y = co-ordinate

c= constant here.

 

 

DDA Algorithm (Digital Differential Analyzer)-

 DDA is a scan conversion line drawing algorithm based on calculating either ∆y or ∆x. 

If the slope is less than or equals to 1 (m<=1), we sample at unit x interval(∆x = 1) and compute each successive y value as yk+1 = yk + m.

Since m can be any real number between 0 and 1, the calculated y value must be rounded to nearest integer. For lines with a positive slope greater than 1 (m>1), we sample at unit y interval(
∆y = 1) and calculate xk+1 = xk + 1/m .

 Advantage:

1. It is simple and easy to understand.

2. This method does not use multiplication theorem.

Disadvantage:

1. It involves floating point additions.

2. Rounding off operations and floating point operations consumes a lot of time.

3. It is less suited for hardware implementation.

Example: If a line is drawn from (2,3) to (6,15) with use of DDA. How many points will needed to generate such line?

Solution: P1(2,3)    P11(6,15)

x1= 2

y1= 3

x2= 6

y2=15

dx= 6-2 = 4

dy= 15-3= 12

m= ∆y/∆x= 12/4 = 3

For calculating next value of x takes x=x+1/m

 

 

 Program: 

from graphics import *
import time
def PutPixle(win, x, y):
    pt = Point(x,y)
    pt.draw(win)
    print(x,y)   
win = GraphWin('DDA Line', 600, 600)
x=int(input("Enter the initial position of X: "))
y=int(input("Enter the initial position of Y: "))
x1=int(input("Enter the final position of X: "))
y1=int(input("Enter the final position of Y: "))
dely = y1-y
delx=x1-x
slope=dely/delx
if slope>1.0:
    while y<y1:
       PutPixle(win, x, y)
       x=x+(1/slope)
       y=y+1.0
else:
    while x<=x1:
       PutPixle(win, x, y)
       y=y+slope
       x=x+1.0
win.getMouse()

 

 Output is generated appropriately.

********************************************************

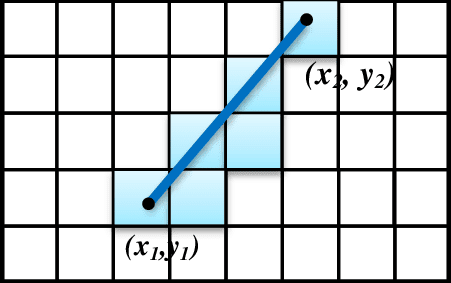
BRESENHAM LINE DRAWING ALGORITHM

An accurate and efficient line generating algorithm developed by Bresenham. It uses incremental interger calculation that can be adopted to draw circle and curves as well.

We first consider the scan conversion process for lines with positive slope less than 1 (m<1).

The pixel positions along a line path are determine by sampling at unit x interval (∆x = 1), plot pixel whose y value is closest to the line path.

Assuming, We have determine that pixel at (xk, yk) is to be displayed, we next need to decide which pixel to plot in column xk+1. Our choices are (xk+1, yk) or (xk+1, yk+1).

y= m(xk +1)+b

then, D1 = y - yk

            = m( xk+1) + b - yk

and 

D2= (yk+1)-y

   = (yk+1) - m( xk+1) - b

then,

D1-D2 =  { m( xk+1) + b - yk } - {(yk+1) - m( xk+1) - b}

           = 2 {m(xk+1) +b -yk}-1

A decision parameter Pk for the Kth step in the algorithm can be determine by- 

Pk = ∆x (D1 - D2)

     =  2 ∆y xk - 2 ∆x yk +c

where c = 2∆y + ∆x (2b -1)

Pk+1 = 2∆y xk+1  - 2∆x yk+1 + c

where c= 2∆y + ∆x (2b -1)

 

Pk+1 - Pk =  2∆y xk+1  - 2∆x yk+1 + c - 2 ∆y xk + 2 ∆x yk - c

where, xk+1 = xk +1

 

 Pk+1 = Pk + 2∆y - 2 ∆x ( yk+1 -yk)

Pk = Pk+1 - 2∆y + 2 ∆x ( yk+1 -yk)
Where the term  ( yk+1 -yk) is either  or 1, depending on the sign of the paramenter Pk.
( yk+1 -yk) is either 0 or 1,
 

Algorithm:

 

The Bresenham algorithm for slope m < 1 

Step 1 − Input the two end-points of line, storing the left end-point in (x0,y0)

Step 2 − Plot the point (x0,y0)

Step 3 − Calculate the constants dx, dy, 2dy, and 2dy–2dx

and get the first value for the decision parameter as −

p0=2dy−dx

Step 4 − At each Xk  along the line, starting at k = 0, perform the following test −

If pk< 0, the next point to plot is (xk+1,yk)

and

pk+1=pk+2dy

Otherwise, the next point to plot is  (xk,yk+1) and,

pk+1=pk+2dy−2dx

Step 5 − Repeat step 4 dx–1times.

For m > 1, find out whether you need to increment x while incrementing y each time.

After solving, the equation for decision parameter Pk        will be very similar, just the x and y in the equation gets interchanged.

Program: 

#include<stdio.h>  
#include<graphics.h>  
void drawline(int x0, int y0, int x1, int y1)  
{  
    int dx, dy, p, x, y;  
    dx=x1-x0;  
    dy=y1-y0;  
    x=x0;  
    y=y0;  
    p=2*dy-dx;  
    while(x<x1)  
    {  
        if(p>=0)  
        {  
            putpixel(x,y,7);  
            y=y+1;  
            p=p+2*dy-2*dx;  
        }  
        else  
        {  
            putpixel(x,y,7);  
            p=p+2*dy;}  
            x=x+1;  
        }  
}  
int main()  
{  
    int gdriver=DETECT, gmode, error, x0, y0, x1, y1;  
    initgraph(&gdriver, &gmode, "c:\\turboc3\\bgi");  
    printf("Enter co-ordinates of first point: ");  
    scanf("%d%d", &x0, &y0);  
    printf("Enter co-ordinates of second point: ");  
    scanf("%d%d", &x1, &y1);  
    drawline(x0, y0, x1, y1);  
    return 0;  
} 

 

Advantage:

1. It involves only integer arithmetic, so it is simple.

2. It avoids the generation of duplicate points.

3. It can be implemented using hardware because it does not use multiplication and division.

4. It is faster as compared to DDA (Digital Differential Analyzer) because it does not involve floating point calculations like DDA Algorithm.

Disadvantage:

1. This algorithm is meant for basic line drawing only Initializing is not a part of Bresenham's line algorithm. So to draw smooth lines, you should want to look into a different algorithm.

 

Example: Starting and Ending position of the line are (1, 1) and (8, 5). Find intermediate points.

Solution: x₁=1
                y₁=1
                x₂=8
                y₂=5
                dx= x₂-x₁=8-1=7
                dy=y₂-y₁=5-1=4
                I₁=2* ∆y=2*4=8
                I₂=2*(∆y-∆x)=2*(4-7)=-6
                d = I₁-∆x=8-7=1

x	y	d=d+I1 or I2
1	1	d+I2=1+(-6)=-5
2	2	d+I1=-5+8=3
3	2	d+I2=3+(-6)=-3
4	3	d+I1=-3+8=5
5	3	d+I2=5+(-6)=-1
6	4	d+I1=-1+8=7
7	4	d+I2=7+(-6)=1
8	5

 

 

 

DDA Algorithm	Bresenham's Line Algorithm
1. DDA Algorithm use floating point, i.e., Real Arithmetic.	1. Bresenham's Line Algorithm use fixed point, i.e., Integer Arithmetic
2. DDA Algorithms uses multiplication & division its operation	2.Bresenham's Line Algorithm uses only subtraction and addition its operation
3. DDA Algorithm is slowly than Bresenham's Line Algorithm in line drawing because it uses real arithmetic (Floating Point operation)	3. Bresenham's Algorithm is faster than DDA Algorithm in line because it involves only addition & subtraction in its calculation and uses only integer arithmetic.
4. DDA Algorithm is not accurate and efficient as Bresenham's Line Algorithm.	4. Bresenham's Line Algorithm is more accurate and efficient at DDA Algorithm.
5.DDA Algorithm can draw circle and curves but are not accurate as Bresenham's Line Algorithm	5. Bresenham's Line Algorithm can draw circle and curves with more accurate than DDA Algorithm.